|
Applications of Matrices and Determinants
|
|
1.1 Introduction |
 |
Zero Matrix |
 |
Ex 1.1.1 (i) Find the Adjoint of 2 x 2 Matrix 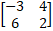 |
 |
Ex 1.1.1 (ii) Find the Adjoint of 3 X 3 Matrix 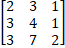 |
 |
Ex 1.1.1 (iii) Adjoint of 3 X 3 Matrix 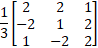 |
 |
Ex 1.1.2 (i) Find the Inverse of 2 x 2 Matrix 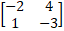 |
 |
Ex 1.1.2 (ii) Find the inverse of 3 X 3 Matrix 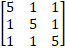 |
 |
Ex 1.1.2 (iii) Find the inverse of 3 X 3 Matrix 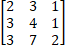 |
 |
Ex 1.1.3 If F(α) = 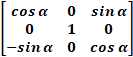 , show
that [F(α)]⁻¹ = F(−α). , show
that [F(α)]⁻¹ = F(−α). |
 |
Ex 1.1.4 If A = 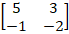 , show that
A² − 3A − 7I₂ = O₂. Hence find A⁻¹. , show that
A² − 3A − 7I₂ = O₂. Hence find A⁻¹. |
 |
Ex 1.1.5 If A = 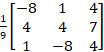 , prove that
A⁻¹ = AT. , prove that
A⁻¹ = AT. |
 |
Ex 1.1.6 If A = 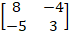 , verify that
A(adj A) = (adj A)A = ∣A∣ I₂. , verify that
A(adj A) = (adj A)A = ∣A∣ I₂. |
 |
Ex 1.1.7 If A = 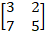 and B = and B =
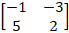 , verify that
(AB)⁻¹
= B⁻¹ A⁻¹. , verify that
(AB)⁻¹
= B⁻¹ A⁻¹.
|
 |
Ex 1.1.8 If adj(A) = 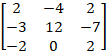 , find A. , find A.
|
 |
Ex 1.1.9 If adj(A) = 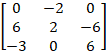 , find
A⁻¹. , find
A⁻¹. |
 |
Ex 1.1.10 Find adj(adj(A)) if adj A = 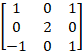 |
 |
Ex 1.1.11 A = 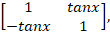 show that
AT A⁻¹ =
show that
AT A⁻¹ = 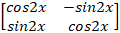 |
 |
Ex 1.1.12 Find the matrix A for which A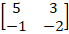 = = 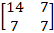 |
 |
Ex 1.1.13 Given A = 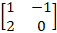 , B = , B =
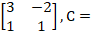 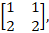 find a matrix X
such that AXB
= C. find a matrix X
such that AXB
= C.
|
 |
Ex 1.1.14 If A = 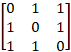 , show that
A⁻¹ = 1/2(A² − 3I). , show that
A⁻¹ = 1/2(A² − 3I). |
 |
Ex 1.1.15 Decrypt the received encoded message [2 −3][20 4] with the encryption
matrix 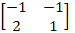 and the
decryption matrix
as its inverse, where the system of codes are described by the numbers 1-26 to the
letters A − Z respectively, and the number 0 to a blank space. and the
decryption matrix
as its inverse, where the system of codes are described by the numbers 1-26 to the
letters A − Z respectively, and the number 0 to a blank space. |
 |
Unit Matrix |
|
1.2 Inverse of a Non-Singular Square Matrix |
 |
Ex 1.2.1 (i) Find the Rank of the Matrix Minor Method 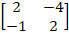 |
 |
Ex 1.2.1 (ii) Find the Rank of the Matrix Minor Method 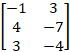 |
 |
Ex 1.2.1 (iii) Find the Rank of the Matrix Minor Method 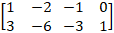 |
 |
Ex 1.2.1 (iv) Find the Rank of the Matrix Minor Method 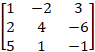 |
 |
Ex 1.2.1 (v) Find the Rank of the Matrix Minor Method 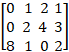 |
 |
Ex 1.2.2 (i) Find the Rank of the Matrix Row Reduction Method 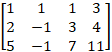 |
 |
Ex 1.2.2 (ii) Find the Rank of the Matrix Row Reduction Method 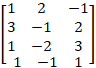 |
 |
Ex 1.2.2 (iii) Find the Rank of the Matrix Row Reduction Method 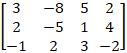 |
 |
Ex 1.2.3 (i) Find the inverse of the Matrix Gauss - Jordan Method 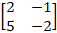 |
 |
Ex 1.2.3 (ii) Find the inverse of the Matrix Gauss - Jordan Method 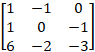 |
 |
Ex 1.2.3 (iii) Find the inverse of the Matrix Gauss - Jordan Method 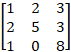 |
 |
Row Echelon Form | Matrices & Determinants |
 |
Transpose of a Matrix |
|
1.3 Elementary Transformations of a Matrix |
|
1.4 Applications of Matrices: Solving System of Linear Equations |
|
1.5 Applications of Matrices: Consistency of system of linear equations by rank method
|
|
2 Complex Numbers |
|
2.1 Introduction to Complex Numbers |
|
2.2 Complex Numbers |
|
2.3 Basic Algebraic Properties of Complex Numbers |
|
2.4 Conjugate of a Complex Number |
|
2.5 Modulus of a Complex Number |
|
2.6 Geometry and Locus of Complex Numbers |
|
2.7 Polar and Euler form of a Complex Number |
|
2.8 de Moivre's Theorem and its Applications |
|
3 Theory of Equations
|
|
3.1 Introduction |
|
3.2 Basics of Polynomial Equations |
|
3.3 Vieta’s Formulae and Formation of Polynomial Equations |
|
3.4 Nature of Roots and Nature of Coefficients of Polynomial Equations |
|
3.5 Applications to Geometrical Problems |
|
3.6 Roots of Higher Degree Polynomial Equations |
|
3.7 Polynomials with Additional Information |
|
3.8 Polynomial Equations with no additional information |
|
3.9 Descartes Rule |
|
4 Inverse Trigonometric Functions |
|
4.1 Introduction |
|
4.2 Some Fundamental Concepts |
|
4.3 Sine Function and Inverse Sine Function |
|
4.4 The Cosine Function and Inverse Cosine Function |
|
4.5 The Tangent Function and the Inverse Tangent Function |
|
4.6 The Cosecant Function and the Inverse Cosecant Function |
|
4.7 The Secant Function and Inverse Secant Function |
|
4.8 The Cotangent Function and the Inverse Cotangent Function |
|
4.9 Principal Value of Inverse Trigonometric Functions |
|
4.10 Properties of Inverse Trigonometric Functions |
|
5 Two Dimensional Analytical Geometry-II |
|
5.1 Introduction |
|
5.2 Circle |
|
5.3 Conics |
|
5.4 Conic Sections |
|
5.5 Parametric form of Conics |
|
5.6 Tangents and Normals to Conics |
|
5.7 Real life Applications of Conics |
|
6 Applications of Vector Algebra |
|
6.1 Introduction |
|
6.2 Geometric Introduction to Vectors |
|
6.3 Scalar Product and Vector Product |
|
6.4 Scalar triple product |
|
6.5 Vector triple product |
|
6.6 Jacobi’s Identity and Lagrange’s Identity |
|
6.7 Different forms of Equation of a Straight line |
|
6.8 Different forms of Equation of a plane |
|
6.9 Image of a point in a plane |
|
6.10 Meeting point of a line and a plane |
|
7 Applications of Differential Calculus |
|
7.1 Introduction |
 |
Ex 7.1.1 A particle moves along a straight line in such a way that after t seconds its
distance from the origin is s = 2t² + 3t metres.
(i) Find the average velocity
between t = 3 and t = 6 seconds.
(ii) Find the instantaneous velocities at t = 3 and
t = 6 seconds. |
 |
Ex 7.1.2 A camera is accidentally knocked off an edge of a cliff 400 ft high. The camera
falls a distance of s=16 t² in t seconds.
(i) How long does the camera fall
before it hits the ground?
(ii) What is the average velocity with which the camera
falls during the last 2 seconds?
(iii) What is the instantaneous velocity of the
camera when it hits the ground? |
|
Ex 7.1.3 A particle moves along a line according to the law s(t) = 2t³ −
9t² + 12t − 4, where t ≥ 0.
(i) At what times the particle changes
direction?
(ii) Find the total distance travelled by the particle in the first 4
seconds.
(iii) Find the particle’s acceleration each time the velocity is zero. |
 |
Ex 7.1.4 If the volume of a cube of side length x is v = x³. Find the rate of
change of the volume with respect to x when x = 5 units. |
 |
Ex 7.1.5 If the mass m(x) (in kilograms) of a thin rod of length x (in metres) is given
by, m(x) = √3x then what is the rate of change of mass with respect to the length
when it is x = 3 and x = 27 metres. |
 |
Ex 7.1.6 A stone is dropped into a pond causing ripples in the form of concentric
circles. The radius r of the outer ripple is increasing at a constant rate at 2 cm per
second. When the radius is 5 cm find the rate of changing of the total area of the
disturbed water? |
 |
Ex 7.1.7 A beacon makes one revolution every 10 seconds. It is located on a ship which
is anchored 5 km from a straight shore line. How fast is the beam moving along the shore
line when it makes an angle of 45° with the shore? |
 |
Ex 7.1.8 A conical water tank with vertex down of 12 metres height has a radius of 5
metres at the top. If water flows into the tank at a rate 10 cubic m/min, how fast is
the depth of the water increases when the water is 8 metres deep? |
 |
Ex 7.1.9 A ladder 17 metre long is leaning against the wall. The base of the ladder is
pulled away from the wall at a rate of 5 m/s. When the base of the ladder is 8 metres
from the wall,
(i) how fast is the top of the ladder moving down the wall?
(ii) at
what rate, the area of the triangle formed by the ladder, wall, and the floor, is
changing? |
 |
Ex 7.1.10 A police jeep, approaching an orthogonal intersection from the northern
direction, is chasing a speeding car that has turned and moving straight east. When the
jeep is 0.6 km north of the intersection and the car is 0.8 km to the east. The police
determine with a radar that the distance between them and the car is increasing at 20
km/hr. If the jeep is moving at 60 km/hr at the instant of measurement, what is the
speed of the car? |
|
7.2 Meaning of Derivatives |
 |
Ex 7.2.1 Find the slope of the tangent to the following curves at the respective given
points.
(i) y = x⁴ + 2x² − x at x = 1
(ii) x = a cos³ t, y = b
sin³ t at t = π/2. |
 |
Ex 7.2.2 Find the point on the curve y = x² − 5x + 4 at which the tangent is
parallel to the line 3x + y = 7. |
 |
Ex 7.2.3 Find the points on the curve y = x³ − 6x² + x + 3 where the normal is
parallel to the line x + y = 1729. |
 |
Ex 7.2.4 Find the points on the curve y² − 4xy = x² + 5 for which the tangent
is horizontal. |
 |
Find the tangent and normal to the following curves at the given points on the
curve.
Ex 7.2.5.1 y = x² − x⁴ at (1, 0) |
 |
Ex 7.2.5.2 y = x⁴ + 2ex at (0, 2) |
 |
Ex 7.2.5.3 y = x sin x at (π/2, π/2) |
 |
Ex 7.2.5.4 x = cos t, y = 2sin² t at t = π/3 |
 |
Ex 7.2.6 Find the equations of the tangents to the curve y = 1 + x³ for which the
tangent is orthogonal with the line x + 12y = 12. |
 |
Ex 7.2.7 Find the equations of the tangents to the curve y = x + 1/x - 1 which are
parallel to the line x + 2y = 6. |
 |
Ex 7.2.8 Find the equation of tangent and normal to the curve given by x = 7 cos t and y
= 2sin t, t ∈ ℝ at any point on the curve. |
 |
Ex 7.2.10 Show that the two curves x² − y² = r² and xy = c² where c,
r are constants, cut orthogonally. |
|
7.3 Mean Value Theorem |
|
7.4 Series Expansions |
|
7.5 Indeterminate Forms |
|
7.6 Applications of First Derivative |
|
7.7 Applications of Second Derivative |
|
7.8 Applications in Optimization |
|
7.9 Symmetry and Asymptotes |
|
7.10 Sketching of Curves |
|
8 Differentials and Partial Derivatives |
|
8.1 Introduction |
|
8.2 Linear Approximation and Differentials |
|
8.3 Functions of Several Variables |
|
8.4 Limit and Continuity of Functions of Two Variables |
|
8.5 Partial Derivatives |
|
8.6 Linear Approximation and Differential of a Function of Several Variables |
|
9 Applications of Integration |
|
9.1 Introduction |
|
9.2 Definite Integral as the Limit of a Sum |
|
9.3 Fundamental Theorems of Integral Calculus and their Applications |
|
9.4 Bernoulli’s Formula |
|
9.5 Improper Integrals |
|
9.6 Reduction Formulae |
|
9.7 Gamma Integral |
|
9.8 Evaluation of Bounded Plane Area by Integration |
|
9.9 Volume of a Solid obtained by Revolving Area about an Axis |
|
10 Ordinary Differential Equations |
|
10.1 Introduction |
|
10.2 Differential Equation, Order, and Degree |
|
10.3 Classification of Differential Equations |
|
10.4 Formation of Differential Equations |
|
10.5 Solution of Ordinary Differential Equations |
|
|
|
10.6 Solution of First Order and First Degree Differential Equations |
|
10.7 First Order Linear Differential Equations |
|
10.8 Applications of First Order Ordinary Differential Equations |
|
11 Probability Distributions |
|
11.1 Introduction |
|
11.2 Random Variable |
|
11.3 Types of Random Variable |
|
11.4 Continuous Distributions |
|
11.5 Mathematical Expectation |
|
11.6 Theoretical Distributions: Some Special Discrete Distributions |
|
12 Discrete Mathematics |
|
12.1 Introduction |
|
12.2 Binary Operations |
|
12.3 Mathematical Logic |